When we cool a metal, suddenly its resistivity drops to zero. Furthermore, the electrons at that state move collectively rather than independently and indicate various interesting properties reflecting this collective motion. This phenomenon providing such a drastic change in metals is called superconductivity and is applied, for example, superstrong electromagnet in the magnetically levitated train and diagnostic imaging unit, magnetic-field sensor, quantum computing device, and electro power cable. Superconducting transition temperature (Tc) below which the system becomes a superconductor is one of the indices of the performance for a superconducting material. Tc is around 10 K or lower for typical materials and this requires a lerge cost for cooling. Therefore, materials having high Tc have been explored. Through that exploreation, magnesium diboride (MgB2, 39 K) and cuprates (about 90 K) were found, and recently, hydrides under a extreamely high pressupre (about 200 K) were found. However, it is challenging to bring the last one under ambient pressure, and such a high-Tc materials stable at a lower pressure is desirable.
Density functional theory for superconductors (SCDFT) is one of the first-principles methods to compute Tc, and it can treat the electron-phonon interaction, electronic Coulomb interaction, and spin fluctuation (SF) fully non-empirically. This method has been applied to mainly the phonon-mediated superconductors. For example, SCDFT is used to reveal the origin of the multiband superconductivity in MgB2, the relationship between the structure and Tc of hydrogen sulfides. We plan to apply this method to a wide variety of materials and accelerate the first-principles exploration of superconductors. For this purpose, we are developing an open-source software Superconducting-Toolkit (SCTK) [1], and release that software on the Web. Also, we perform a benchmark to the simplest superconductors and non-superconductors, namely 35 elemental metals [2]; we formulate a method to treat SF together with the spin-orbit interaction (SOI) and investigate these two effects on Tc (see figure). This benchmark will be a milestone for exploring superconductors with high-throughput computations and methodological improvements in the future.
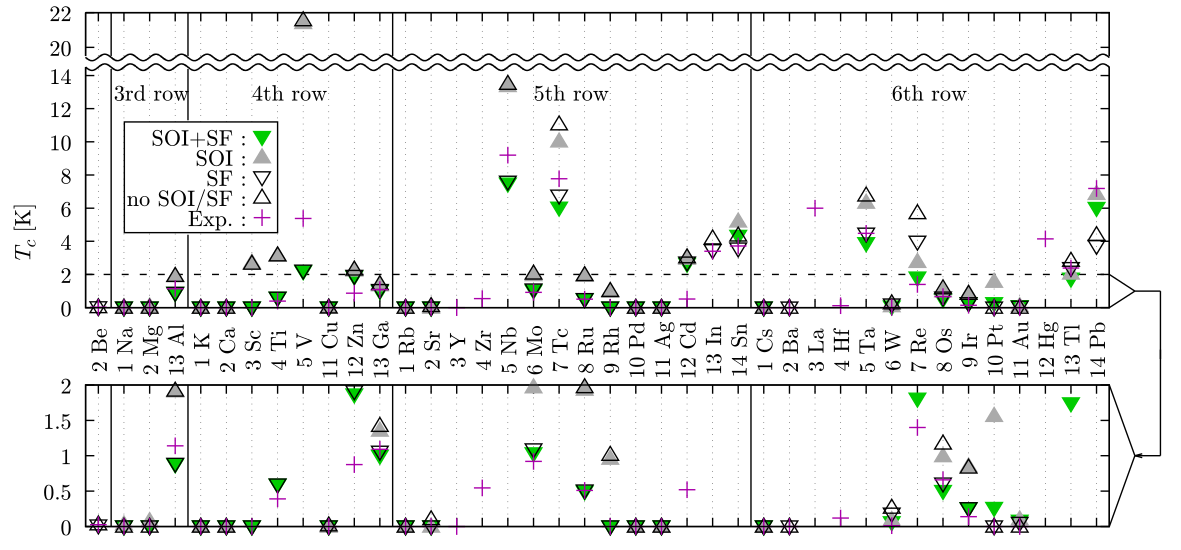Calculated and experimental Tc (from Ref. [2])
Other than Tc, SCDFT can obtain the superconducting gap of the Bogoliumv-de-Gennes-Kohn-Sham system. Although this gap function is not guaranteed to be identical to the gap observed in the experiments, such as the tunneling conductance and ultrasonic attenuation, it is empirically known that such an SCDFT gap is used for a qualitative analysis of weak-coupling superconductors. As an example of such an analysis, the gap function of MgB2 has different values for each Fermi surface as expected by experiments. This multi-band superconductivity comes from the fact that each Fermi surface consists of different electronic bonding states, and the band with stronger electron-phonon interaction has a larger superconducting gap function. Also in YNi2B2C, anisotropic superconducting gaps appears because of the variation of the character of electronic states on Fermi surfaces. In this case, the gap function varies continuously on a Fermi surface; we revealed that this varying gap function is negatively correlated to the contribution from Ni d states to the Kohn-Sham orbitals [3].